外を見ていて必ず目に入ります。『雲』です。
今回気になってしまったものはそんなものです。つまり、
『車窓から見る雲ってどこに浮いている雲なんやろ?』
気になったからには、昔の数学などを引っ張り出してきて色々考えてきました。
まず前提条件として、
・地球の直径は赤道面で12748kmの完全な球形。
・いる場所は北緯30度(正確には明石で35度だそうですが)として直径は8498km(赤道面の2/3)
・雲は高度2000mのところを見ている(雨雲は500~2000m程度だそうです)
と仮定していろいろやってみました。で結果。
#1 力技(写真の左の図)。
パワポで、直径84.98cmの円(地表面:青)と85.00cmの円(雲の高さ:赤)を作ります。地表面の円の接線を引き雲の円までの距離が1.77cm、つまり、約177km先の空となります。
数学もくそもない(笑)。
#2 数学っぽい話。
『三平方の定理』を利用して・・・覚えてますかね??直角三角形の線の長さの求め方です。
直角を挟んだ2線をx、y、残った斜辺をzとするとx二乗+y二乗=z二乗のあれです。
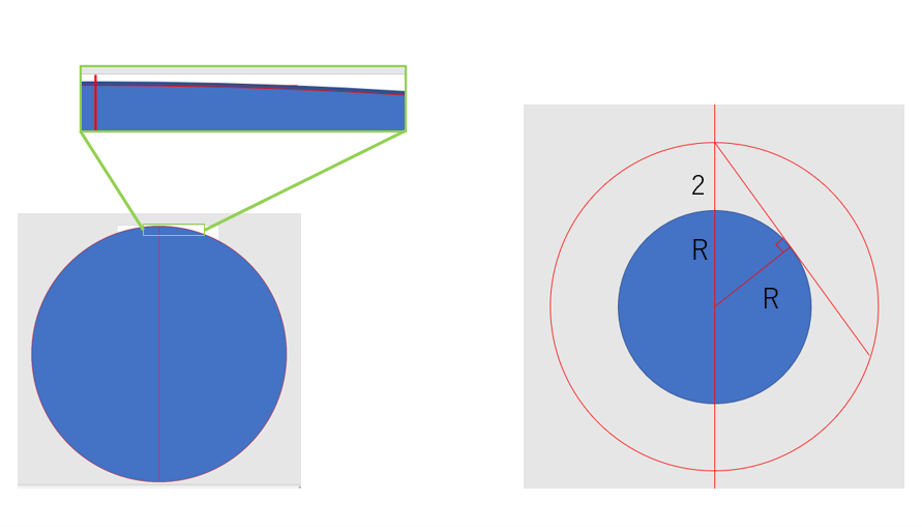
縮尺はめちゃくちゃですが右の図です。
右上の直角三角形を利用します。右上の直角の部分に立っていると仮定して、地表の接線上で真横を見ます。(高さが地表から2km)で計算すると・・・
R二乗+x二乗=(R+2)二乗になります。(注:数学的には、Rは直径、半径はrで表していたような・・・もう図は作っちゃったので見逃して~)
x=√(4R+4)
R=4249を代入して
x≒130.4km
概算ですが#2は大きくはズレていないハズです。個人的には#1の力技の方をやってみたかったので、二つの答えがほぼ同じであればうれしかったですが。残念ながら力技では誤差が大きめでした。部屋に直径85cmの円を鉛筆で描けばもう少し精度は上がるかもしれません。また、リハ室のベッドを全部避けて8.5mの円を描けばもっと・・・(以下略)。そんな円を描くのも大変ですので、これが限界でした。
結論:130kmほど向こうの空の雲を見ているんだろうな~でした。
そこで地図を引っ張り出して・・・大阪市を中心に半径130kmくらいの円を地図に反映させてみました(スーパーマップル関西道路地図参照)。
北は若狭湾のど真ん中・・・だったので、少し西にズらせば丹後半島の北端くらい、東にズらせば(北北東くらい)敦賀市です。真東も伊勢湾の中ですが、少し北にズらせば知多半島のひげみたいなところにセントレア空港、南(東南東)にズらせば志摩半島です。真南だとぎりぎり紀伊半島の南端くらい(白浜空港よりは南)です。真西もまた瀬戸内海なので、ちょっと北で小豆島、南西方向なら淡路島を超えて徳島市でした。
この円周上には近畿地方がほぼなく、個人的な印象では意外と遠くなんやな~と。
ま、大阪市は日本有数の低地なので、四方見渡せばどの方角も高い障害物があるはずです。見た感じ山の上に雲があるので実際に見ている雲はもっと近いのでしょう。
中川和也 拝